How to Read Box and Whisker Plots
Understanding Boxplots
![]()

The epitome higher up is a boxplot. A boxplot is a standardized way of displaying the distribution of data based on a five number summary ("minimum", first quartile (Q1), median, 3rd quartile (Q3), and "maximum"). It can tell you nearly your outliers and what their values are. It can also tell y'all if your data is symmetrical, how tightly your data is grouped, and if and how your information is skewed.
This tutorial will include:
- What is a boxplot?
- Understanding the anatomy of a boxplot past comparing a boxplot against the probability density function for a normal distribution.
- How do you make and interpret boxplots using Python?
As e'er, the code used to make the graphs is available on my github. With that, let'southward get started!
What is a Boxplot?
For som e distributions/datasets, you will notice that you need more information than the measures of central trend (median, mean, and way).

You need to take data on the variability or dispersion of the data. A boxplot is a graph that gives you a good indication of how the values in the data are spread out. Although boxplots may seem primitive in comparing to a histogram or density plot, they have the reward of taking up less space, which is useful when comparing distributions betwixt many groups or datasets.

Boxplots are a standardized way of displaying the distribution of information based on a 5 number summary ("minimum", get-go quartile (Q1), median, third quartile (Q3), and "maximum").
median (Q2/50th Percentile): the middle value of the dataset.
commencement quartile (Q1/25th Percentile): the middle number between the smallest number (not the "minimum") and the median of the dataset.
third quartile (Q3/75th Percentile): the center value betwixt the median and the highest value (not the "maximum") of the dataset.
interquartile range (IQR): 25th to the 75th percentile.
whiskers (shown in blue)
outliers (shown equally dark-green circles)
"maximum": Q3 + 1.five*IQR
"minimum": Q1 -ane.five*IQR
What defines an outlier, "minimum", or"maximum" may not exist clear yet. The side by side department volition try to clear that upwardly for you.
Boxplot on a Normal Distribution
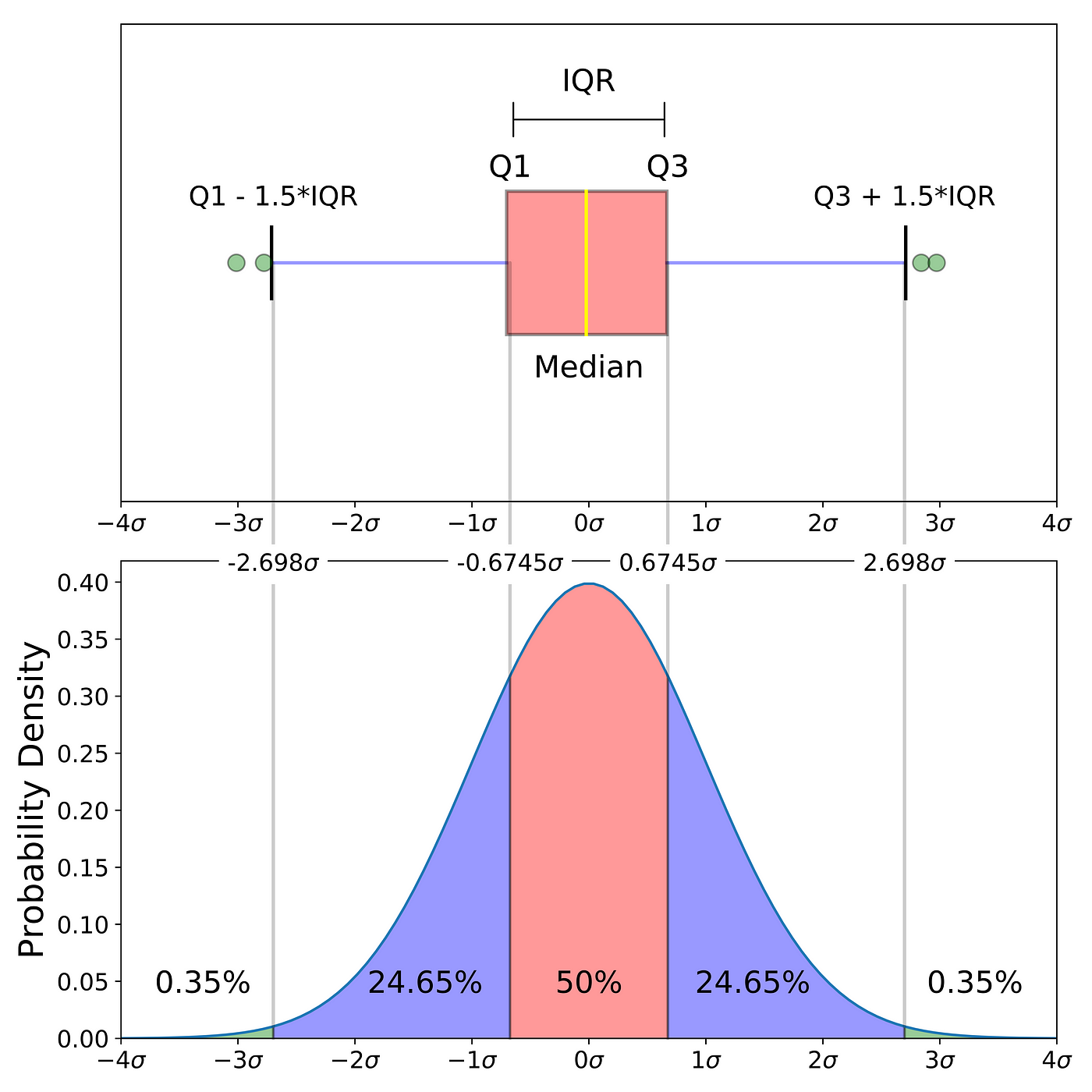
The paradigm above is a comparison of a boxplot of a nearly normal distribution and the probability density function (pdf) for a normal distribution. The reason why I am showing you this epitome is that looking at a statistical distribution is more commonplace than looking at a box plot. In other words, it might help you understand a boxplot.
This section will comprehend many things including:
- How outliers are (for a normal distribution) .7% of the data.
- What a "minimum" and a "maximum" are
Probability Density Function
This role of the post is very similar to the 68–95–99.7 rule article, but adapted for a boxplot. To exist able to understand where the percentages come from, it is of import to know virtually the probability density function (PDF). A PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on any ane value. This probability is given by the integral of this variable's PDF over that range — that is, it is given by the surface area under the density function only above the horizontal axis and between the lowest and greatest values of the range. This definition might not make much sense so permit's clear it up past graphing the probability density function for a normal distribution. The equation below is the probability density function for a normal distribution
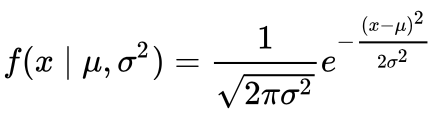
Permit's simplify it past bold we have a mean (μ) of 0 and a standard deviation (σ) of 1.

This can be graphed using anything, but I choose to graph it using Python.
# Import all libraries for this portion of the blog post
from scipy.integrate import quad
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline x = np.linspace(-4, 4, num = 100)
constant = ane.0 / np.sqrt(2*np.pi)
pdf_normal_distribution = abiding * np.exp((-x**2) / 2.0)
fig, ax = plt.subplots(figsize=(10, five));
ax.plot(x, pdf_normal_distribution);
ax.set_ylim(0);
ax.set_title('Normal Distribution', size = twenty);
ax.set_ylabel('Probability Density', size = 20);
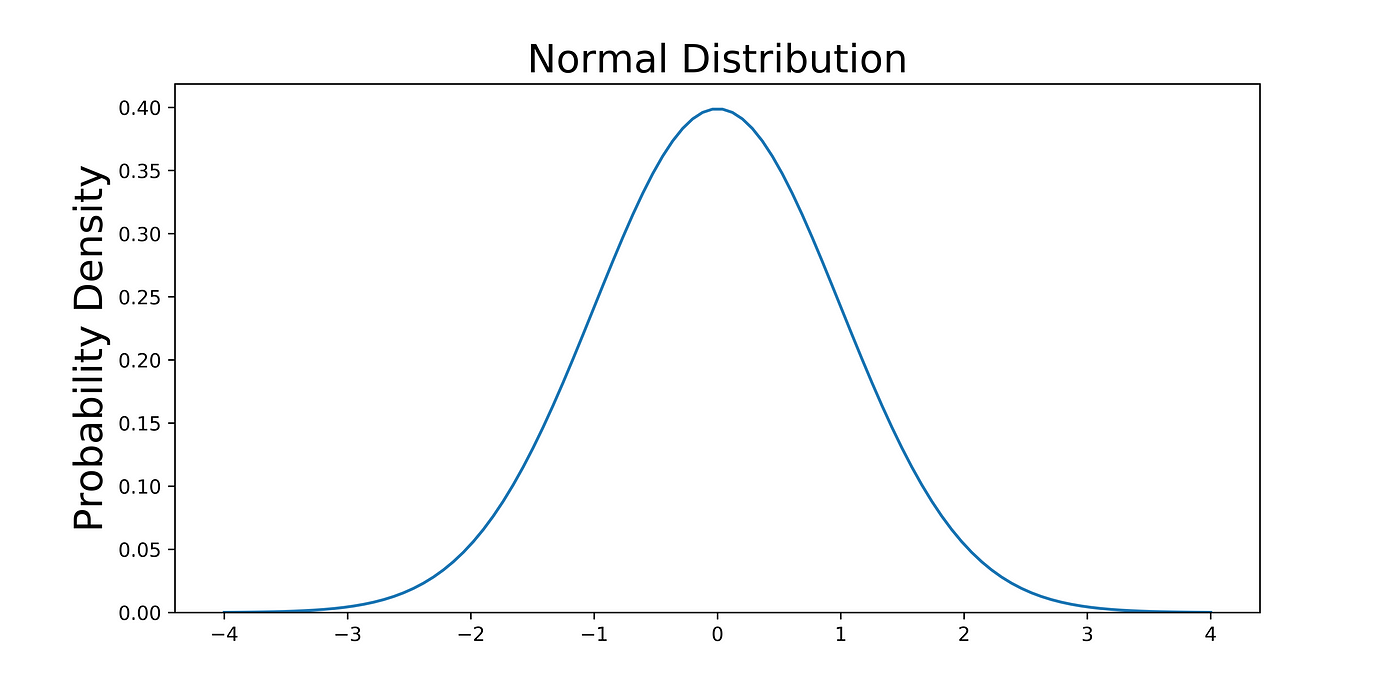
The graph above does not show y'all the probability of events but their probability density. To become the probability of an issue within a given range we will need to integrate. Suppose we are interested in finding the probability of a random information bespeak landing inside the interquartile range .6745 standard deviation of the hateful, we need to integrate from -.6745 to .6745. This can exist washed with SciPy.
# Brand PDF for the normal distribution a function
def normalProbabilityDensity(ten):
constant = ane.0 / np.sqrt(ii*np.pi)
return(constant * np.exp((-x**2) / two.0) ) # Integrate PDF from -.6745 to .6745
result_50p, _ = quad(normalProbabilityDensity, -.6745, .6745, limit = chiliad)
impress(result_50p)

The same can be done for "minimum" and "maximum".
# Make a PDF for the normal distribution a function
def normalProbabilityDensity(x):
constant = ane.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) ) # Integrate PDF from -ii.698 to 2.698
result_99_3p, _ = quad(normalProbabilityDensity,
-ii.698,
2.698,
limit = g)
print(result_99_3p)
Equally mentioned earlier, outliers are the remaining .vii% percentage of the data.
It is of import to annotation that for any PDF, the area under the bend must be 1 (the probability of drawing whatsoever number from the function's range is always 1).

Graphing and Interpreting a Boxplot
This section is largely based on a free preview video from my Python for Information Visualization grade. In the final section, we went over a boxplot on a normal distribution, simply as you obviously won't always have an underlying normal distribution, permit's go over how to utilise a boxplot on a real dataset. To do this, we will use the Chest Cancer Wisconsin (Diagnostic) Dataset. If you don't have a Kaggle account, you can download the dataset from my github.
Read in the data
The lawmaking below reads the data into a pandas dataframe.
import pandas as pd
import seaborn every bit sns
import matplotlib.pyplot as plt # Put dataset on my github repo
df = pd.read_csv('https://raw.githubusercontent.com/mGalarnyk/Python_Tutorials/master/Kaggle/BreastCancerWisconsin/data/information.csv')
Graph Boxplot
A boxplot is used below to analyze the relationship between a categorical feature (cancerous or benign tumor) and a continuous feature (area_mean).
In that location are a couple ways to graph a boxplot through Python. You tin graph a boxplot through seaborn, matplotlib, or pandas.
seaborn
The code below passes the pandas dataframe df into seaborn's boxplot.
sns.boxplot(x='diagnosis', y='area_mean', data=df) 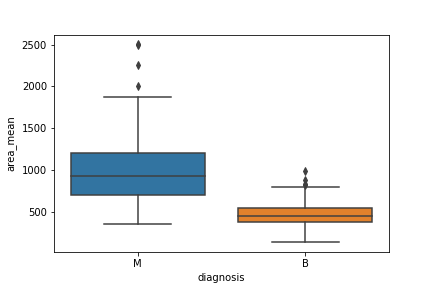
matplotlib
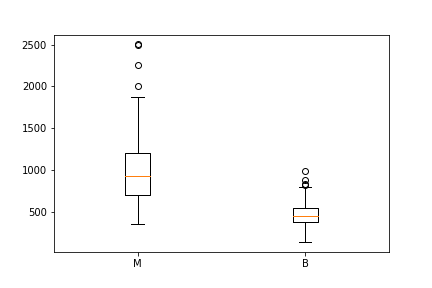
The boxplots yous accept seen in this post were made through matplotlib. This arroyo can be far more tiresome, but tin can requite y'all a greater level of control.
malignant = df[df['diagnosis']=='1000']['area_mean']
benign = df[df['diagnosis']=='B']['area_mean'] fig = plt.figure()
ax = fig.add_subplot(111)
ax.boxplot([cancerous,benign], labels=['M', 'B'])
pandas
You tin plot a boxplot by invoking .boxplot() on your DataFrame. The code beneath makes a boxplot of the area_mean column with respect to different diagnosis.
df.boxplot(column = 'area_mean', by = 'diagnosis');
plt.championship('') 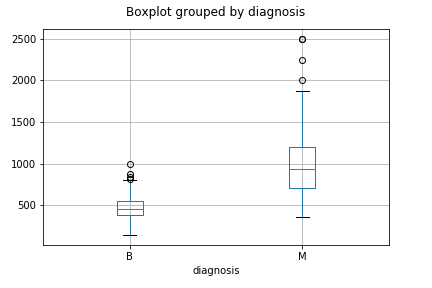
Notched Boxplot
The notched boxplot allows you to evaluate confidence intervals (by default 95% confidence interval) for the medians of each boxplot.
cancerous = df[df['diagnosis']=='1000']['area_mean']
benign = df[df['diagnosis']=='B']['area_mean'] fig = plt.effigy()
ax = fig.add_subplot(111)
ax.boxplot([cancerous,benign], notch = True, labels=['G', 'B']);

Interpreting a Boxplot
Data science is about communicating results so keep in mind you can ever brand your boxplots a bit prettier with a little scrap of work (code here).
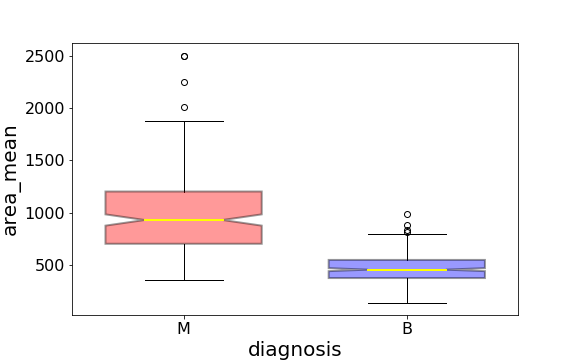
Using the graph, we can compare the range and distribution of the area_mean for cancerous and benign diagnosis. We observe that there is a greater variability for malignant tumor area_mean too equally larger outliers.
Too, since the notches in the boxplots practise not overlap, you can conclude that with 95% confidence, that the truthful medians do differ.
Here are a few other things to proceed in heed about boxplots:
- Keep in heed that you can always pull out the data from the boxplot in instance you want to know what the numerical values are for the unlike parts of a boxplot.
- Matplotlib does not approximate a normal distribution kickoff and calculates the quartiles from the estimated distribution parameters. The median and the quartiles are calculated directly from the data. In other words, your boxplot may look different depending on the distribution of your information and the size of the sample, e.chiliad., asymmetric and with more or less outliers.
Conclusion
Hopefully this wasn't too much information on boxplots. Futurity tutorials will take some this knowledge and go over how to use it to agreement conviction intervals. My next tutorial goes over How to Employ and Create a Z Table (standard normal table). If you any questions or thoughts on the tutorial, feel free to accomplish out in the comments below, through the YouTube video page, or through Twitter.
Source: https://towardsdatascience.com/understanding-boxplots-5e2df7bcbd51
0 Response to "How to Read Box and Whisker Plots"
Post a Comment